A függvény kifejezéssel biztosan találkoztál már a középiskolában is. A közgazdaságtan megkerülhetetlen részét teszik ki eme kreálmányok: beszélhetünk kereslet vagy kínálat, de akár bevétel vagy költség függvényekről is (ezeket egyelőre csak említés szintjén hoztam fel).
A függvény (definíció szerint) egy egyértelmű hozzárendelés, azaz vannak x-ek és ezekhez egyesével hozzárendelünk egy-egy y-t (de pontosan csak egyet – ezt jelenti az egyértelmű).
Fontos, hogy a függvények képét MINDIG balról jobbra nézzük és elemezzük.
Azt, hogy milyen x-ek jöhetnek szóba, az értelmezési tartomány határozza meg (Df – D, mint domain), míg azt, hogy milyen y-ok, azt pedig az értékkészlet (Rf – R, mint range).
Magát a függvényt szokták jelölni egy betűvel is, mint f= vagy g=, időnként hozzákötnek egy x-et is: f(x)= vagy g(x)= (ezzel fejezik ki, hogy x-től függ a függvényérték – ez a későbbiekben, amikor már kétváltozós függvények lesznek (x és y is változó és ezektől függ a z), fontosabb szerepet kap).
Sokféle függvényről beszélhetünk, ezek közül csak néhány olyat fogok bemutatni ebben a posztban, amelyek a gazdasági képzéseken gyakran előkerülnek.
Lineáris függvény
A lineáris függvényeket nagyon röviden úgy lehetne jellemezni, hogy nincs bennünk görbület, csak egyszerűen egy egyenesről beszélünk.
Konstans függvény
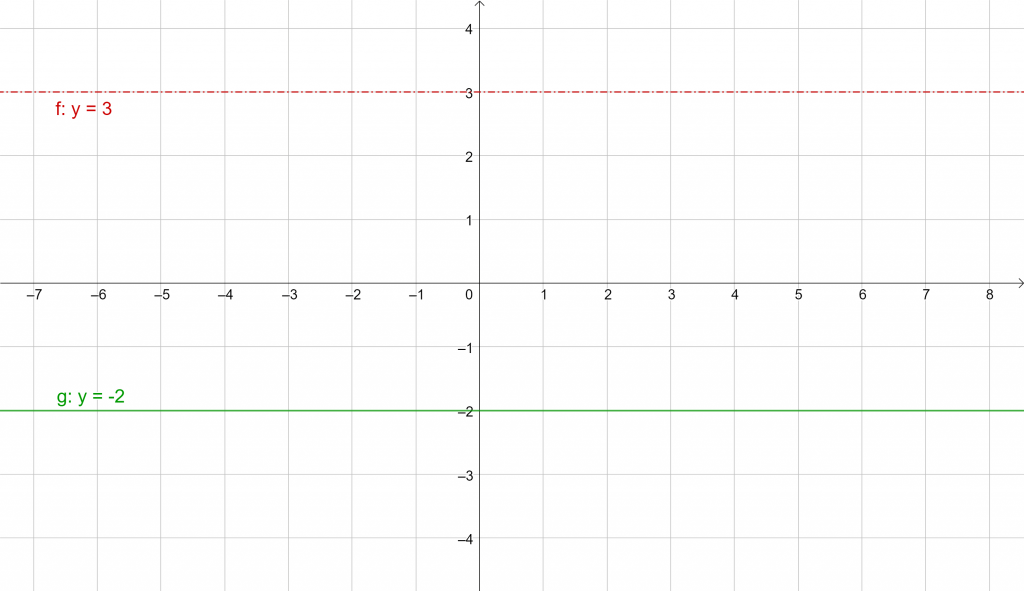
Egy speciális fajtája a lineáris függvényeknek a konstans függvény, ami minden egyes x-hez azonos y-t rendel hozzá. Ezt felismerni, illetve felvázolni egy vízszintes egyenessel lehet. A lenti ábrán a piros függvény esetén látható, hogy minden x-hez a 3-as y-t rendeli, míg a zöld esetén minden x-hez a -2-es y-t.
Elsőfokú függvény
A lineáris függvények gyakrabban előforduló fajtája az elsőfokú függvény, aminek általános formája:
f(x) = a*x + b

Ahol az “a” tag fejezi ki a függvény meredekségét (röviden: ha a függvény mentén kilépünk egyet jobbra, akkor mennyit kell felfele vagy lefele menni, kicsit csúnyábban: ha az x-et egy egységgel növeljük, akkor ehhez az y mekkora nagyságú változása tartozik), míg a “b” tag a függvény y-tengellyel vett metszéspontját (kicsit csúnyábban: ha az x=0, akkor ahhoz milyen y tartozik). Ezen tagokat sokféle különböző betűvel szokták jelölni, statisztikában például b0-val a “b” tagot, míg b1-el az “a” tagot, de ugyanazt fejezik ki (annyi különbséggel, hogy statisztikában már konkrét, köznapi jelentést is fogunk tudni (és kell is!) társítani ezekhez – erről bővebben majd később).
Pozitív meredekségű az egyenes (azaz növekvő a függvényünk), ha az “a” tag pozitív (az ábrán a lila és a barna függvények) és negatív meredekségű (azaz csökkenő a függvényünk), ha az “a” tag negatív (az ábrán a szürke függvény).
Másodfokú függvény
A jó kis parabolák biztosan rémlenek még. A másodfokú függvények általános formája:
f(x) = a*x2 + b*x + c
(ahol az a≠0, hiszen ha a=0, akkor nem beszélhetünk másodfokú függvényről)

A függvényben lévő “a” tag előjele adja meg, hogy a parabola szomorú vagy vidám. Ha az “a” tag előtt egy negatív szám áll, akkor a parabola szomorú (lefelé nyitott), ha pedig az “a” tag előtt egy pozitív számot látunk, akkor a parabola vidám (felfelé nyitott). Ha pedig ezeket le tudjuk olvasni, akkor a függvény monotonitásának megállapítása sem fog a későbbiekben gondot okozni (erről bővebben később).
Ha az “a” tag abszolút értéke 1-nél nagyobb, akkor a parabola egyre jobban összecsukódik, míg ha az “a” abszolút értéke 1-nél kisebb, akkor a parabola egyre jobban szétnyílik (nézd az ábrán a zöld és a piros függvényeket).
A teljes négyzetté alakítás segítségével (IDE kattintva találsz hozzá segítséget) könnyen meg tudjuk adni a függvény szélsőértékét (ami lehet maximum vagy minimum) – a teljes függvényvizsgálatról ITT olvashatsz.
Exponenciális függvény
Az exponenciális függvény onnan ismerhető fel könnyen, hogy az ismeretlen vagy változó (általában x) a kitevőben (fent) található. Általános alakja:
f(x) = ax
(ahol az “a” pozitív valós szám, kivéve az 1-et, mert ha a=1, akkor nem beszélhetünk exponenciális függvényről)

Ha az “a” tag 1-től nagyobb, akkor egy szigorúan monoton növekvő, míg ha az “a” tag 0<a<1 közötti, akkor egy szigorúan monoton csökkenő függvénnyel van dolgunk.
Az exponenciális függvény “növekedésének logikáját” a kamatos kamattal lehetne a legjobban jellemezni: beteszünk egy adott összeget, amire a bank kamatot fizet. Az első évben csak a befizetett összegre kapjuk a kamatot, ám a későbbi években mindig a kamattal növelt befizetett összegre fizet újabb és újabb kamatot (az ábrán a piros és zöld függvények).
Ha a “csökkenésének értelmét” keressük, akkor pl. a cégek gépeinek értékcsökkenését érdemes röviden átnézni. Megvásárolunk egy számítógépet egy összegért, aminek értéke (mivel használjuk minden nap levelezésre, nyomtatásra, számlakiállításra stb…) folyamatosan csökken. Természetesen az első évben a kezdeti érték csökken bizonyos %-kal, míg a rá következő években már a korábbi, csökkent érték fog még tovább és tovább csökkenni (az ábrán a kék és narancssárga függvények).
A fenti függvényfajtákon kívül is rengeteg féle létezik, például abszolútérték, logaritmus vagy trigonometrikus, de ezek nem jellemzőek az egyetemi gazdasági képzésekben, így nem tárgyaljuk őket. A törtfüggvények ugyan előkerülnek a képzés során, ezek általános jellemzése nem adható meg ilyen egyszerűen, mint a fentieké, így ezeket az adott témaköröknél fogjuk átnézni.





