
3. témakör – Deriválás
Gazdasági matematika 1.
A differenciálszámítás, vagy más néven deriválás egy függvény adott pontjába húzott érintőjének a meredekségét adja meg. Na jó, és ez miért jó, mire használható? Ez így valóban csak egy üres, száraz definíció, de ha elolvasod ezt a bejegyzést és nyomon követed a következő heti anyagokat is, meg fogsz világosodni GARANTÁLTAN! 😉
Mire jó a deriválás (na nem az életben, hanem a matekban)?
A deriválást a függvényelemzésnél tudod majd alkalmazni, ugyanis egy függvény első deriváltjából megmondható a függvény monotonitása és szélsőértéke, míg egy függvény második deriváltjából a konvexitás és az inflexiós pont. Ne rohanjunk ennyire előre, nézzük át a deriválás alapjait.
A differenciálszámítást nem szabad úgy felfogni, mint egy megértésre szoruló anyagrészt – ahhoz, hogy átmenj Gazdmatek1-ből, elegendő, ha alkalmazni tudod a képlettárban is található deriválási szabályokat. A képlettárat ZH közben is használhatod, ám nem árt a gyakorlás, mert önmagában a négyjegyű függvénytábla sem csinálja meg senki helyett az jeles matek érettségit, hiába van benne minden „tudás”.
Kezdjünk el deriválni – avagy az elemi alapfüggvények deriváltja
Tudom ám, hogy csak erre a részre vágytál… kívánságod pedig parancs! 😉 A deriválása jelölése egy ’ jellel (aposztróf) történik. Ha például az f(x) függvényt deriválod, ez lesz belőle: f ’ (x)
Konstans függvény
Minden konstans deriváltja pontosan 0, ám nem csak olyan egyszerű formáikban jelennek meg, mint például az f(x) = 3, hanem az f(x)=3² vagy éppen az f(x) = lg8 is egy konstans, csak éppen más alakjában.

Hatványfüggvény
Az f(x)=xª függvény deriválásakor a kitevőt (a) lehozzuk az alap (x) elé, a kitevő értékét pedig fent 1-el csökkentjük. Ami nehezítés lehet, hogy időnként alkalmazni kell a deriválás előtt a hatványazonosságokat vagy el kell tüntetni a gyökjelet. Erről ITT találsz néhány videót.

Logaritmus függvény
Az a-alapú logaritmus x esetén a derivált az alább látható, míg az lnx egy speciális esetén, aminek a deriváltja az 1/x.

Exponenciális függvény
Az a^x és az e^x deriváltja alább látható. Igen, ez utóbbit könnyű lesz megjegyezni. 🙂
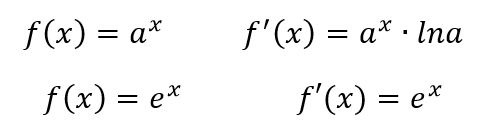
Mire jók a fentiek és miként lehet a ZH-ban?
A fenti elemi alapfüggvények deriváltjai csak bevezetnek a deriválásba, de a ZH-ban természetesen nem ilyen egyszerű példák lesznek jelen. A deriválási szabályokat (szorzás és osztás), valamint egy összetett függvény deriválását is a következő videóból ismerheted meg:
Tetszett a bejegyzés és a videó?
Ha IGEN a válaszod, akkor lájkold a Mádi Matek Facebook-oldalát a további INGYENES anyagokért, vagy iratkozz fel a hírlevélre, amihez ZH felkészülési tippek és ajándék MINTA ZH is jár. 🙂



