Az egyetemi matekban a hatványazonosságok ismerete és alkalmazása amolyan alap, tehát ezeket elvárják és külön már nem értékelik az oktatók, ám a különböző feladatok megoldása során (pl. deriválás vagy később erre épülően a függvényelemzés) elengedhetetlen, hogy ezeket pontosan tudd és használd.
Csak, hogy biztosan azonos fogalmakra gondoljunk, álljon itt egy kép:
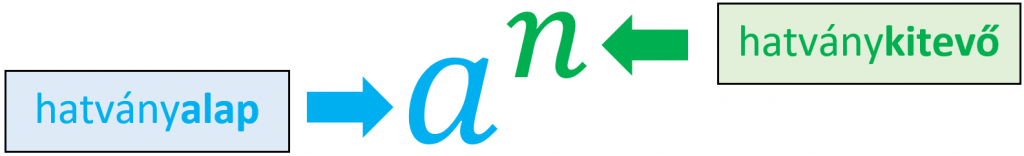
Azonos alapú hatványokkal végzett műveletek
Azonos alapú hatványok szorzása

Két (vagy több) azonos alapú hatvány szorzása úgy történik, hogy a hatványkitevőket összeadjuk. Igen, tudom, hogy furcsa, hogy bár szorzás van közöttük, de mégis összeadódnak a kitevők – ilyen ez a matek. 🙂
Azonos alapú hatványok osztása/hányadosa

Két (vagy több) azonos alapú hatvány osztása úgy történik, hogy a hatványkitevőket kivonjuk – a számláló (felső tag) kitevőjéből a nevező (alsó tag) kitevőjét.
Azonos kitevőjű hatványokkal végzett műveletek
Azonos kitevőjű hatványok szorzása

Két (vagy több) azonos kitevőjű hatvány szorzása úgy történik, hogy a hatványalapokat összeszorozzuk és ezt a szorzatot emeljük a (közös és egyben azonos) kitevőre.
Azonos kitevőjű hatványok osztása/hányadosa

Két (vagy több) azonos kitevőjű hatvány osztása úgy történik, hogy a hatványalapokat elosztjuk és ezt a hányadost (törtet) emeljük a (közös és egyben azonos) kitevőre.
Hatvány hatványozása

Hatvány hatványozása úgy történik, hogy a hatványkitevőket összeszorozzuk.
Gyökvonás azonosságok
Kezdjük itt is az alapfogalmakkal:

Azonos gyökkitevőjű hatványok szorzása

Két (vagy több) azonos gyökkitevőjű hatvány szorzása úgy történik, hogy a két hatvány szorzatát a közös gyökkitevő alá hozzuk.
Azonos gyökkitevőjű hatványok osztása

Két (vagy több) azonos gyökkitevőjű hatvány osztása úgy történik, hogy a két hatvány hányadosát a közös gyökkitevő alá hozzuk.
Gyökjel eltüntetése
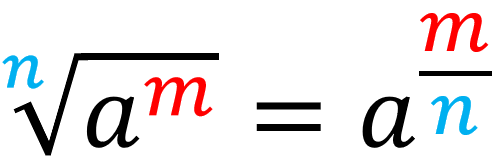
Egy tetszőleges gyök alatti hatvány esetén a gyökjel eltüntethető, ha a gyök alatti hatvány kitevőjét elosztjuk a gyökkitevővel.
Egymásba ágyazott gyökök összevonása

Egymásba ágyazott (értsd: egymás alatti) gyökök összevonása úgy történik, hogy a hatványt a gyökkitevők szorzatának gyöke alá vonjuk.
Érdekelne néhány konkrét példa is, hogy ezeket hogyan kell alkalmazni?
Készítettem ehhez a bejegyzéshez egy oktatóvideót is, ahol mindegyik hatványazonosságra mutatok egy-egy példát.





